前言:
大家都知道float和double會有誤差
但原因是什麼呢?
今天就跟大家分享Float和Double會誤差的原因
一. 浮點數介紹
一開始先對於float和double做身家調查
浮點類型的範圍
| 類型 | 最小值 | 最大值 |
|---|---|---|
| float | 1.175494351 E – 38 | 3.402823466 E + 38 |
| double | 2.2250738585072014 E – 308 | 1.7976931348623158 E + 308 |
浮點類型
| 類型 | 有效數字 | 位元組數 |
|---|---|---|
| float | 6 – 7 | 4 |
| double | 15 – 16 | 8 |
二. 浮點數產生
以float來說可以儲存4 byte = 32 bit 是說最多可以存32個 0 or 1
但 float 和 int都是 32 bit 使用方式卻完全不一樣
浮點數計算方式是由 IEEE 754 進位浮點數算術標準創立
他把浮點數分成三部分 Sign(符號), Exponent(指數), Mantissa(尾數) 來表示他的值**
表示方式 1111 1111 1111 1111 1111 1111 1111 1111
Sign(符號) 第1個 bit (紅色)
- 0 = 正數
- 1 = 負數
Exponent(指數) 第2個 ~ 第9個 bit (藍色)
- 總共8 bit 最大值 255 (二進至值)
- 127 為中間值原點
Mantissa(尾數) 第10個 ~ 第32個 bit (棕色)
- 計算之後的尾數
到目前因該是有看沒有懂XD
等等帶個範例大家就會比較清楚了
三. 實例解說
後面看到 X 代表等待計算的值
12.5f 為例子 如何計算出 32 bit 如何儲存這個值?
判斷是正數還是負數決定Sign(符號)
- 因為12.5f是正數
0XXX XXXX XXXX XXXX XXXX XXXX XXXX XXXX
- 因為12.5f是正數
計算Exponent(指數)
- 將12.5f轉成二進制 12.5f = 1100.1
- **將數值底數變成 ****1<底數<2 ****1100.1 = 1.1001 * 2 ^ 3 **
- 2^3 二的三次方就是 指數要加的值 127 + 3 = 130 (1000 0010)
- *1011 1111 1XXX XXXX XXXX XXXX XXXX XXXX
- *0000 0001 1XXX XXXX XXXX XXXX XXXX XXXX
- *———————————————————————–
- *1100 0001 0XXX XXXX XXXX XXXX XXXX XXXX
Mantissa(尾數) 計算
- 最後將
1.1001小數點後的值.1001追加到(指數)後面
- ** 1100 0001 0000 0000 0000 0000 0000 0000 **
- + 0000 0000 0100 1000 0000 0000 0000 0000
- —————————————————————
- ** 0100 0001 0100 1000 0000 0000 0000 0000**
- 最後將
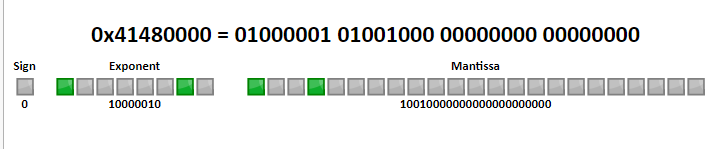
所以我們可以得出 12.5f 在 32bit 中是
這裡有個工具 Float (IEEE754 Single precision 32-bit) 可以方便我們來驗算值是否正確
他很貼心幫我們列出 ** Sign(符號), Exponent(指數), Mantissa(尾數) ** 位置給我們對應
四,為什麼會不精準
現在我們知道計算 Exponent(指數) 需要將值轉成二進制 ,但如果是12.53f 轉成二進制會變成這樣1100.100000111100111....... 極限值就會和原本的值出現誤差
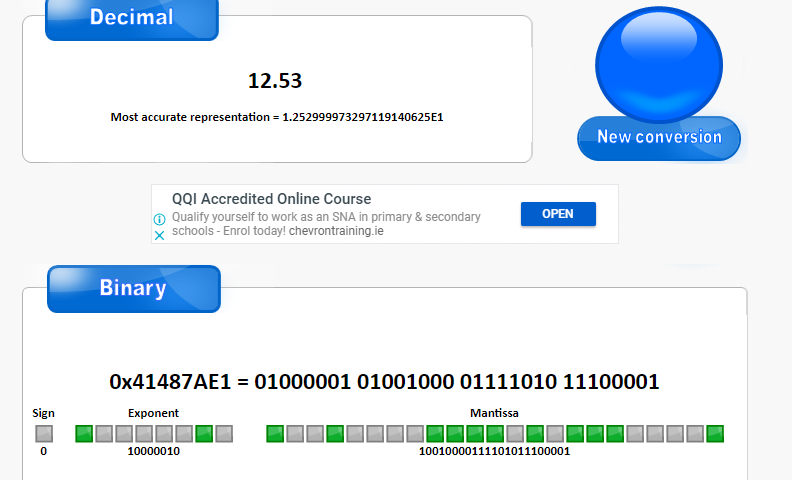
如圖 我們可以看到 12.53f 其實會變成 1.252999973297119140625E1 這就是float不準確的原因
float介紹完了 double和float概念一樣只是儲存空間更大而已^^
小結
因為為了節省空間浮點數 使用特別儲存方式來節省空間,有一好沒兩好這樣就少了精準度
此文作者:Daniel Shih(石頭)
此文地址: https://isdaniel.github.io/float-double/
版權聲明:本博客所有文章除特別聲明外,均採用 CC BY-NC-SA 3.0 TW 許可協議。轉載請註明出處!
